Using The Horizontal Line Test To Determine If A Function Has An Inverse Function

By dinosaurse On Aug 26, 2025

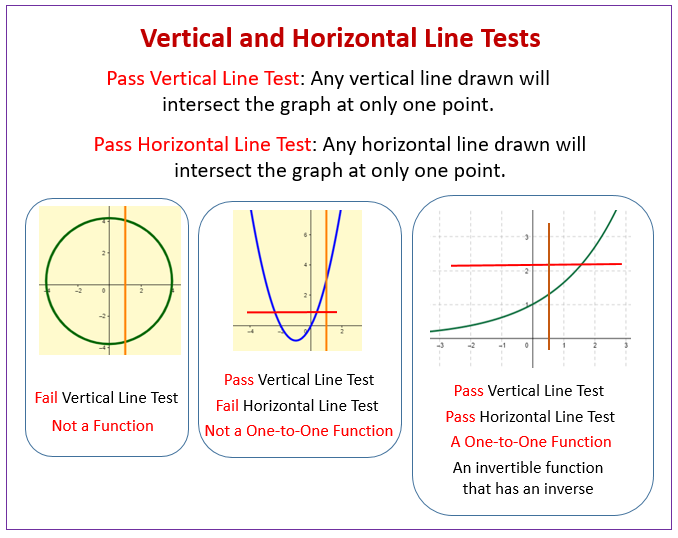
Inverse Functions Examples Solutions Videos Activities This video demonstrates how to use the horizontal line test to determine whether or not the function is 1 to 1 and to determine whether or not the function has an inverse function . Learn what the horizontal line test is and how it can help you check if the inverse of a function is a function. see examples of functions that pass the test!.

Ppt Determine Whether The Inverse Of A Function Is A Function The horizontal line test is a simple, visual way to tell if your function has an inverse function. it’s useful because it tells us whether a function is one to one or not. more on that in a moment. another benefit is that you get to draw with a colored pencil – a rare treat in math!. To determine if a function has an inverse, we can use the horizontal line test with its graph. if any horizontal line drawn crosses the function more than once, then the function has no inverse. for a function to have an inverse, each output of the function must be produced by a single input. Use the horizontal line test to determine whether or not the function y = x3 graphed below is invertible. for the first graph of y = x3, no horizontal line intersects graph of f more than once. therefore, f is invertible. Learning objectives determine the conditions for when a function has an inverse. use the horizontal line test to recognize when a function is one to one. find the inverse of a given function. draw the graph of an inverse function. evaluate inverse trigonometric functions.

Inverse Functions Ppt Download Use the horizontal line test to determine whether or not the function y = x3 graphed below is invertible. for the first graph of y = x3, no horizontal line intersects graph of f more than once. therefore, f is invertible. Learning objectives determine the conditions for when a function has an inverse. use the horizontal line test to recognize when a function is one to one. find the inverse of a given function. draw the graph of an inverse function. evaluate inverse trigonometric functions. Learn to determine if two functions are inverses, apply the horizontal line test effectively, and use algebraic methods to solve for inverses. this approach will enhance comprehension of function behavior and the skills necessary to manipulate and analyze mathematical functions. This lesson explores the horizontal line test, a crucial tool in precalculus for determining whether the inverse of a function is also a function. through visual examples and clear explanations, students will learn how to apply this test and understand its implications for function invertibility. If a function passes the horizontal line test, we know it is injective and that a left inverse exists. therefore, the horizontal line test can best be thought of as a criterion for the existence of a left inverse, which is necessary but not sufficient for a two sided inverse. Example # 1: use the horizontal line test to determine if the given function has an inverse; if it does, then find that inverse and determine the domain and range of the function & its inverse; and graph the results.

Inverse Functions Algebra Iii Sec 1 9 Objective Ppt Download Learn to determine if two functions are inverses, apply the horizontal line test effectively, and use algebraic methods to solve for inverses. this approach will enhance comprehension of function behavior and the skills necessary to manipulate and analyze mathematical functions. This lesson explores the horizontal line test, a crucial tool in precalculus for determining whether the inverse of a function is also a function. through visual examples and clear explanations, students will learn how to apply this test and understand its implications for function invertibility. If a function passes the horizontal line test, we know it is injective and that a left inverse exists. therefore, the horizontal line test can best be thought of as a criterion for the existence of a left inverse, which is necessary but not sufficient for a two sided inverse. Example # 1: use the horizontal line test to determine if the given function has an inverse; if it does, then find that inverse and determine the domain and range of the function & its inverse; and graph the results.

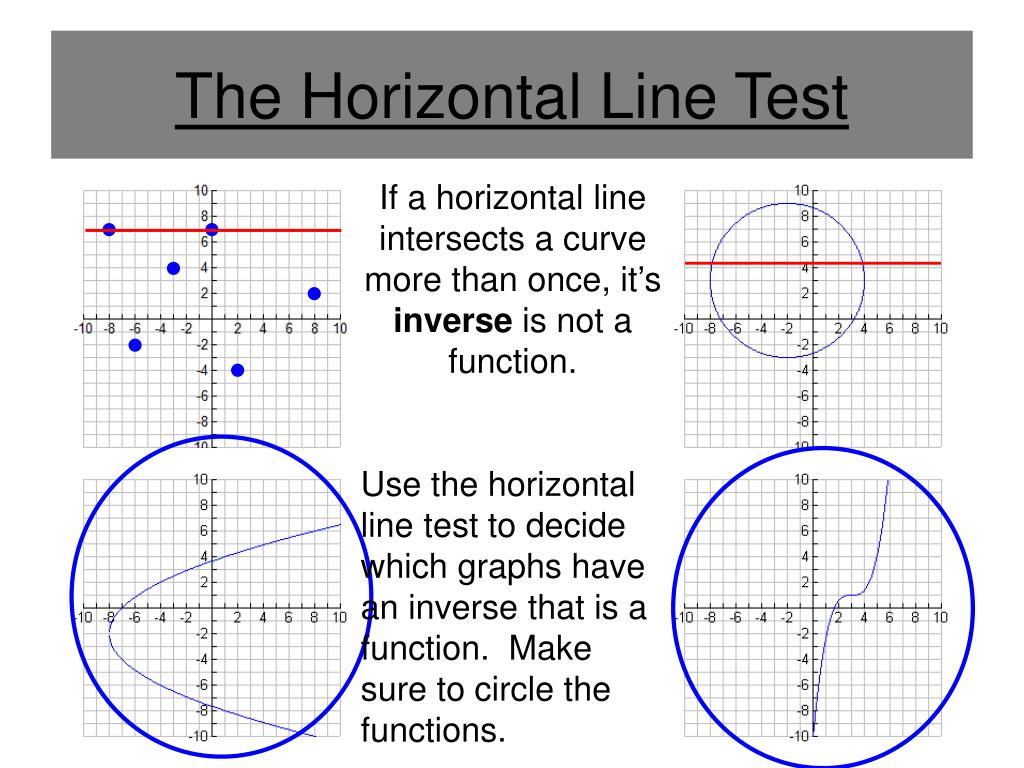
Ppt Inverse Functions Powerpoint Presentation Free Download Id 2633927 If a function passes the horizontal line test, we know it is injective and that a left inverse exists. therefore, the horizontal line test can best be thought of as a criterion for the existence of a left inverse, which is necessary but not sufficient for a two sided inverse. Example # 1: use the horizontal line test to determine if the given function has an inverse; if it does, then find that inverse and determine the domain and range of the function & its inverse; and graph the results.

Using The Horizontal Line Test To Determine If A Function Has An

Step into a realm of limitless possibilities with our blog. We understand that the online world can be overwhelming, with countless sources vying for your attention. That's why we stand out by providing well-researched, high-quality content that educates and entertains. Our blog covers a diverse range of interests, ensuring that there's something for everyone. From practical how-to guides to in-depth analyses and thought-provoking discussions, we're committed to providing you with valuable information that resonates with your passions and keeps you informed. But our blog is more than just a collection of articles. It's a community of like-minded individuals who come together to share thoughts, ideas, and experiences. We encourage you to engage with our content, leave comments, and connect with fellow readers who share your interests. Together, let's embark on a quest for continuous learning and personal growth.

Using the Horizontal Line Test to Determine if a Function has an Inverse Function

Using the Horizontal Line Test to Determine if a Function has an Inverse Function

Using the Horizontal Line Test to Determine if a Function has an Inverse Function Inverse Relations & Horizontal Line Test Horizontal Line Test and One to One Functions How to determine if a function graph has an inverse and if the inverse is a function Use the Horizontal Line Test to Determine if a Function has an Inverse Function Using the horizontal line test to determine if an inverse is a function Horizontal Line Test To Determine Whether A Function Is One To One | PreCalculus Horizontal Line Test: Inverses and One To One Functions Sum & Difference Identities for Cosine Example Problems - Part 1 Using the horizontal line test to determine if an inverse is a function Using vertical and horizontal line tests to determine if graphs are one-to-one functions Determine whether the function has an inverse function Using the Horizontal Line Test to Determine if a Function is One to One The Horizontal Line Test 3.7.2 Horizontal Line Test And Derermining If a Function Has an Inverse Function Inverse Functions - Horizontal line test What is the condition for a function to have an inverse function? (pass horizontal line test) Using the horizontal line test to see if a function is one-to-one Inverse Functions and Horizontal Line Test Using the horizontal line test

Conclusion

Taking a closer look at the subject, one can see that the post shares pertinent understanding in connection with Using The Horizontal Line Test To Determine If A Function Has An Inverse Function. In the entirety of the article, the author exhibits significant acumen pertaining to the theme. Notably, the chapter on key components stands out as a highlight. The writer carefully articulates how these features complement one another to create a comprehensive understanding of Using The Horizontal Line Test To Determine If A Function Has An Inverse Function.

Further, the write-up does a great job in simplifying complex concepts in an accessible manner. This clarity makes the subject matter beneficial regardless of prior expertise. The author further amplifies the investigation by adding pertinent illustrations and practical implementations that place in context the intellectual principles.

An additional feature that distinguishes this content is the in-depth research of diverse opinions related to Using The Horizontal Line Test To Determine If A Function Has An Inverse Function. By investigating these multiple standpoints, the article gives a fair picture of the theme. The meticulousness with which the author tackles the theme is highly praiseworthy and sets a high standard for analogous content in this field.

To summarize, this content not only educates the audience about Using The Horizontal Line Test To Determine If A Function Has An Inverse Function, but also motivates further exploration into this interesting theme. If you happen to be just starting out or an authority, you will come across worthwhile information in this thorough piece. Gratitude for taking the time to this detailed post. If you would like to know more, please do not hesitate to contact me via our messaging system. I am eager to hearing from you. To deepen your understanding, you can see a few associated write-ups that might be beneficial and enhancing to this exploration. Wishing you enjoyable reading!