Solved Use The Horizontal Line Test To Determine Whether The Chegg

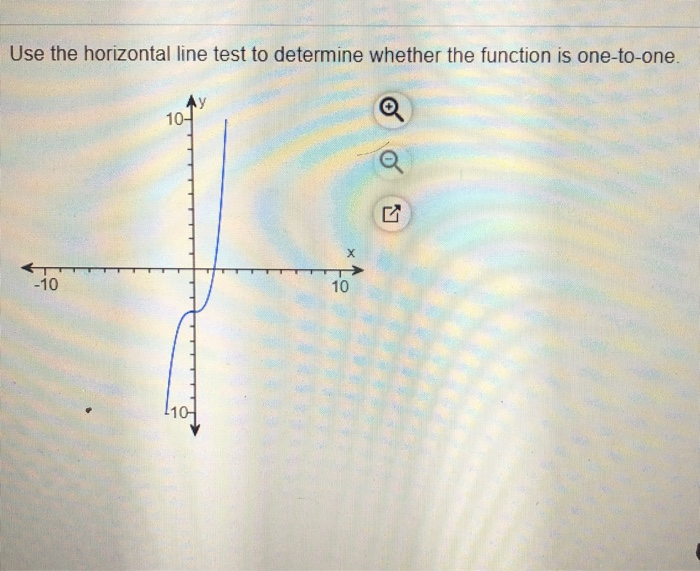
Solved Use The Horizontal Line Test To Determine Whether The Chegg Question: use the horizontal line test to determine whether the function is oneto one. use the horizontal line test to determine whether the function is oneto one. there’s just one step to solve this. The horizontal line test is a method used to determine whether a function is one to one. if a horizontal line intersects the graph of the function at more than one point, then the function is not one to one.

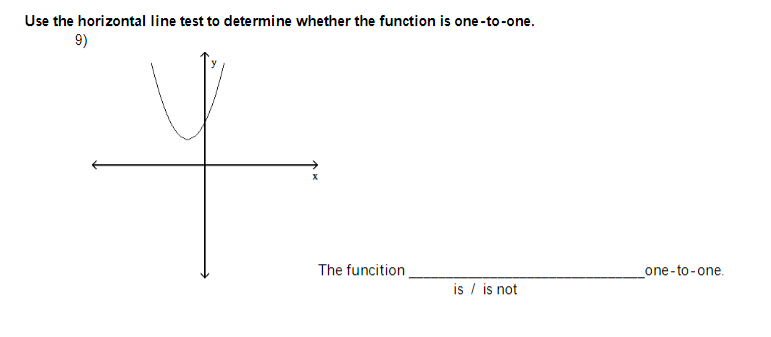
Solved Use The Horizontal Line Test To Determine Whether The Chegg In simple terms, if you can draw a horizontal line across a graph and it only touches the graph at one point, then the function is one to one. this is known as the horizontal line test. if any horizontal line crosses the graph of the function more than once, the function is not one to one. Video answer: so in this problem, we're looking to see whether the vertical line test indicates whether whether the horizontal line tests are determines whether function is 1 to 1. Using the horizontal line test we will examine whether the given function has an inverse function. since we know that a function has an inverse function if and only if it is one to one, we will therefore examine what is required. In this lesson, we will delve into the concept of one to one functions and explore a method called the horizontal line test to determine if a function is one to one.

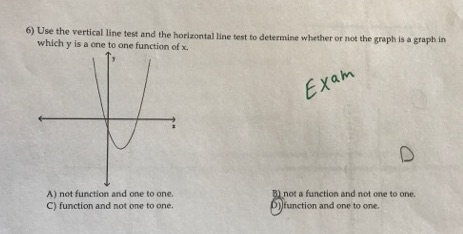
Solved Use The Vertical Line Test And The Horizontal Line Chegg Using the horizontal line test we will examine whether the given function has an inverse function. since we know that a function has an inverse function if and only if it is one to one, we will therefore examine what is required. In this lesson, we will delve into the concept of one to one functions and explore a method called the horizontal line test to determine if a function is one to one. Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. using the horizontal line test, determine whether the function is one to one. is the function one to one? here’s the best way to solve it. Find step by step calculus solutions and your answer to the following textbook question: in each part, use the horizontal line test to determine whether the function f is one to one. f (x) = square root of (x 1). One effective way to determine if a function is one to one is by using the **horizontal line test**. this test involves drawing horizontal lines across the graph of the function. if any horizontal line touches the graph more than once, the function is not one to one. Learn to determine if two functions are inverses, apply the horizontal line test effectively, and use algebraic methods to solve for inverses. this approach will enhance comprehension of function behavior and the skills necessary to manipulate and analyze mathematical functions.

Solved Which Test Do We Use To Determine Whether A Given Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. using the horizontal line test, determine whether the function is one to one. is the function one to one? here’s the best way to solve it. Find step by step calculus solutions and your answer to the following textbook question: in each part, use the horizontal line test to determine whether the function f is one to one. f (x) = square root of (x 1). One effective way to determine if a function is one to one is by using the **horizontal line test**. this test involves drawing horizontal lines across the graph of the function. if any horizontal line touches the graph more than once, the function is not one to one. Learn to determine if two functions are inverses, apply the horizontal line test effectively, and use algebraic methods to solve for inverses. this approach will enhance comprehension of function behavior and the skills necessary to manipulate and analyze mathematical functions.