3 Find The Closest Point To Y In The Subspace W Spanned By V1 And Vz And Find The Distance From Y

Solved Find The Closest Point To Y In The Subspace W Spanned Chegg The question is a linear algebra problem where we are asked to find the closest point to a given vector in a subspace spanned by two other vectors. we solve it using the projection formula and substituting the provided vectors into the formula. To find the closest point to y in the subspace w spanned by u1 and u2, it's required to calculate the scalar projections of vector y on vectors u1 and u2 which are denoted as (: y, u1:) and (: y, u2:).

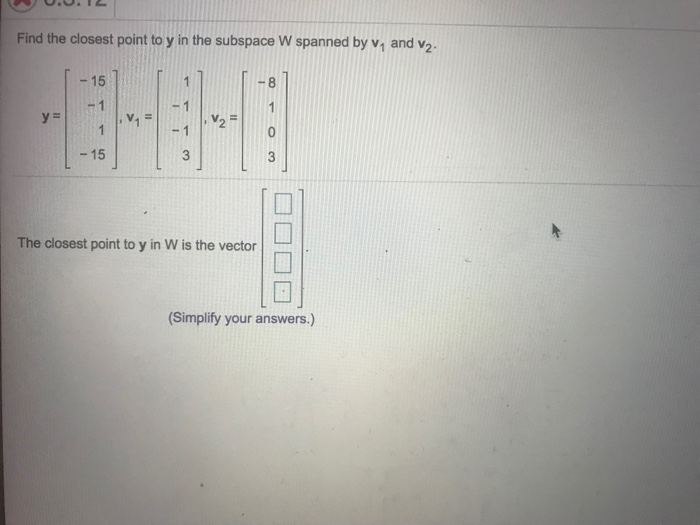
Solved Find The Closest Point To Y In The Subspace Spanned Chegg To do the calculations, take the dot product of $ (*)$ with both $\\w 1$ and $\\w 2$, remembering that the dot products with $\\w$ will be zero. We have solutions for lay's linear algebra and its applications, 5th edition, including chapter 6.3 problem 16e. get high quality textbook solutions here. And since every orthogonal set is linearly independent therefore we get the set {u 1, u 2} \ {\mathbf {u 1},\mathbf {u 2}\} {u1 ,u2 } is an orthogonal basis for the subspace w w w. The distance from point y to the subspace w is found using the formula ∣∣y −p ∣∣, where p is the closest point in w. to calculate p, project y onto the subspace spanned by the given vectors.

Solved Find The Closest Point To Y In The Subspace W Spanned By V1 And And since every orthogonal set is linearly independent therefore we get the set {u 1, u 2} \ {\mathbf {u 1},\mathbf {u 2}\} {u1 ,u2 } is an orthogonal basis for the subspace w w w. The distance from point y to the subspace w is found using the formula ∣∣y −p ∣∣, where p is the closest point in w. to calculate p, project y onto the subspace spanned by the given vectors. Math algebra algebra questions and answers find the closest point to y in the subspace w spanned by v1 and v2. the closest point to y in w is tge vector. Let's say the vectors v1 and v2 are given, and y is the point we're interested in. the subspace w is spanned by v1 and v2, which means any point in w can be written as a linear combination of v1 and v2. To find the distance from the point y to the subspace w spanned by the vectors v1 and v2 , we need to follow a few steps. given that the closest point in w to y is y^ , the distance can be computed using the formula for the distance between two points in a euclidean space. There’s just one step to solve this.