Tangents Drawn From External Point To Circle Are Equal Theorem 10 2

Theorem 10 2 Class 10 Tangents From External Point Of Circle Are Given: let circle be with centre o and p be a point outside circle pq and pr are two tangents to circle intersecting at point q and r respectively to prove: lengths of tangents are equal i.e. pq = pr construction: join oq , or and op proof: as pq is a tangent oq ⊥ pq so, ∠ oqp = 90° similarly, pr is a tangent & or ⊥ pr so, ∠ orp = 90. Problem 1: two tangents are drawn from an external point on a circle of area 3 cm. find the area of the quadrilateral formed by the two radii of the circle and two tangents if the distance between the centre of the circle and the external point is 5 cm. solution:.

Class 10 Theorem 10 2 The Lengths Of Tangent Drawn From An External After understanding theorem 10.2, you can solve the exercise questions given in the ncert book of class 10 maths. the lengths of tangents drawn from an external point to a circle are equal. given. ap and aq are two tangents from point a to a circle o. to prove. ap=aq. construction. join oa, op, and oq. proof. Theorem 10.2 : the lengths of tangents drawn from an external point to a circle are equal. in this tutorial, you will find the explanation of the following: more. Step by step video, text & image solution for theorem 10.2 : the lengths of tangents drawn from an external point to a circle are equal. by maths experts to help you in doubts & scoring excellent marks in class 10 exams. abcd is a quadrilateral in which a circle is inscribed. Theorem: suppose that two tangents are drawn to a circle s from an exterior point p. let the points of contact be a and b, as shown: our current theorem says that: the lengths of these two tangents will be equal, that is, pa = pb.

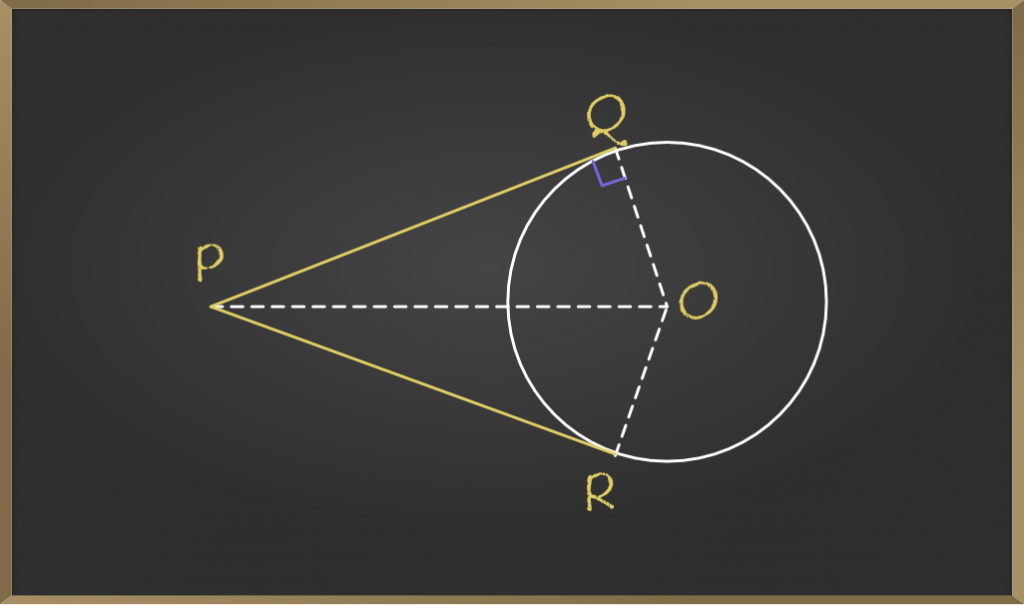
Theorem The Lengths Of Tangents Drawn From An External Point To A Step by step video, text & image solution for theorem 10.2 : the lengths of tangents drawn from an external point to a circle are equal. by maths experts to help you in doubts & scoring excellent marks in class 10 exams. abcd is a quadrilateral in which a circle is inscribed. Theorem: suppose that two tangents are drawn to a circle s from an exterior point p. let the points of contact be a and b, as shown: our current theorem says that: the lengths of these two tangents will be equal, that is, pa = pb. To prove that the lengths of the tangents drawn from an external point to a circle are equal, i.e., pq = pr. connect the center o to the external point p (op). connect the center o to the points of tangency q and r (oq and or). Lengths of two tangents drawn from an external point to a circle are equal. given: ap and aq are two tangents drawn from a point a to a circle c (o, r). to prove: ap = aq. construction: join op, oq and oa. proof: in Δaoq and Δapo. ∠oqp = ∠opa [tangent at any point of a circle is perp. to radius through the point of contact] ao = ao [common]. Hence, tangents drawn from an external point to a circle are of equal length. note: this question can also be solved by using a property that the line joining the center of a circle and an external point from which the tangents are drawn is the angle bisector. The document discusses theorem 10.2 from chapter 10 of class 10 circles, stating that the lengths of tangents drawn from an external point to a circle are equal. it is authored by davneet singh, an experienced educator in maths, science, and computer science.

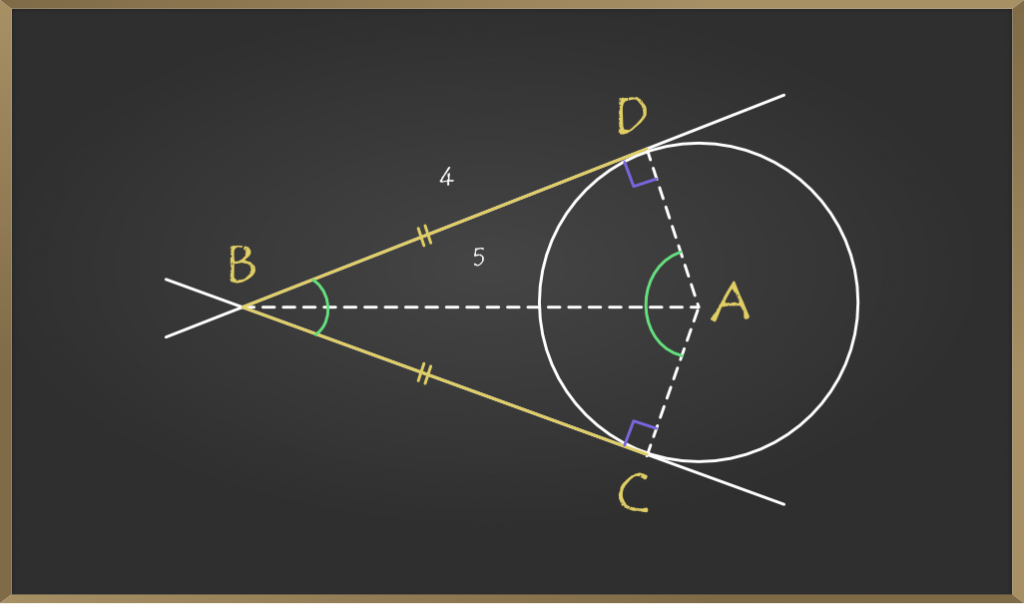
Theorem The Lengths Of Tangents Drawn From An External Point To A To prove that the lengths of the tangents drawn from an external point to a circle are equal, i.e., pq = pr. connect the center o to the external point p (op). connect the center o to the points of tangency q and r (oq and or). Lengths of two tangents drawn from an external point to a circle are equal. given: ap and aq are two tangents drawn from a point a to a circle c (o, r). to prove: ap = aq. construction: join op, oq and oa. proof: in Δaoq and Δapo. ∠oqp = ∠opa [tangent at any point of a circle is perp. to radius through the point of contact] ao = ao [common]. Hence, tangents drawn from an external point to a circle are of equal length. note: this question can also be solved by using a property that the line joining the center of a circle and an external point from which the tangents are drawn is the angle bisector. The document discusses theorem 10.2 from chapter 10 of class 10 circles, stating that the lengths of tangents drawn from an external point to a circle are equal. it is authored by davneet singh, an experienced educator in maths, science, and computer science.

Theorem 10 2 Class 10 Tangents From External Point Of Circle Are Hence, tangents drawn from an external point to a circle are of equal length. note: this question can also be solved by using a property that the line joining the center of a circle and an external point from which the tangents are drawn is the angle bisector. The document discusses theorem 10.2 from chapter 10 of class 10 circles, stating that the lengths of tangents drawn from an external point to a circle are equal. it is authored by davneet singh, an experienced educator in maths, science, and computer science.