Solved Using The Fact That Congruence Modulo M Is An Chegg Com

Solved Using The Fact That Congruence Modulo M is An | Chegg.com

Solved Using The Fact That Congruence Modulo M is An | Chegg.com Using the fact that congruence modulo m is an equivalence relation on z and without reference to theorems 3.2.2 and 3.2.4, prove that for all x,yinz : [mlo9 2, mlo9 3] (e) if x‾∩bar (y)≠o?, then x‾?b=ar (y). In this section, we define congruence modulo m on the set of integers. we give some properties and prove results that allow us to solve or simplify some congruence relations.

Using The Fact That Congruence Modulo M is An | Chegg.com

Using The Fact That Congruence Modulo M is An | Chegg.com We say two integers are in the same congruence class if they are congruent modulo m. we write [x] for the congruence class containing x, that is, the set of integers congruent to x modulo m. the set of congruence classes mod m are denoted by zm. zm consists of m distinct classes: [0], [1], [2], , [m – 1]. Modular arithmetic is the “arithmetic of remainders.” the somewhat surprising fact is that modular arithmetic obeys most of the same laws that ordinary arithmetic does. this explains, for instance, homework exercise 1.1.4 on the associativity of remainders. Using the fact that congruence modulo m is an equivalence relation on z and without reference to theorems 3.2.2 and 3.2.4, prove that for all x and y in 7 (a) xex. A good first step is to recall the formal definition of $a \bmod m$ more specifically, to recall the formal definition previously given by whoever stated the theorem, because that will give specific steps to take. in fact there are five different definitions on the page alone!.

Congruence Modulo M | PDF | Integer | Algebra

Congruence Modulo M | PDF | Integer | Algebra Using the fact that congruence modulo m is an equivalence relation on z and without reference to theorems 3.2.2 and 3.2.4, prove that for all x and y in 7 (a) xex. A good first step is to recall the formal definition of $a \bmod m$ more specifically, to recall the formal definition previously given by whoever stated the theorem, because that will give specific steps to take. in fact there are five different definitions on the page alone!. Instead of writing n = mq r, we can use the congruence notation in the following way. we say that n is congruent to r modulo m, if n = mq r for some integer q. Step 1: given that congruence modulo m is an equivalence relation on z, we know that it satisfies the properties of reflexivity, symmetry, and transitivity. show more…. To summarize: solving for x in the congruence ax 1 mod m is equivalent to solving for integers x and y in the equation ax my = 1 (be sure you see why!), and the latter equation can be solved without any guesswork by reversing euclid's algorithm on a and m when (a; m) = 1. Recall: the congruence modulo m on z is an equivalence relation and the equivalence class of z e z, {ує z : y x (mod m)) of z. claim: now one can prove that if tn proof.

Solved Show That The Congruence Relation, Modulo M, Is An | Chegg.com

Solved Show That The Congruence Relation, Modulo M, Is An | Chegg.com Instead of writing n = mq r, we can use the congruence notation in the following way. we say that n is congruent to r modulo m, if n = mq r for some integer q. Step 1: given that congruence modulo m is an equivalence relation on z, we know that it satisfies the properties of reflexivity, symmetry, and transitivity. show more…. To summarize: solving for x in the congruence ax 1 mod m is equivalent to solving for integers x and y in the equation ax my = 1 (be sure you see why!), and the latter equation can be solved without any guesswork by reversing euclid's algorithm on a and m when (a; m) = 1. Recall: the congruence modulo m on z is an equivalence relation and the equivalence class of z e z, {ує z : y x (mod m)) of z. claim: now one can prove that if tn proof.

Solved 3.) () Define The Relation: "congruence Modulo N" On | Chegg.com

Solved 3.) () Define The Relation: "congruence Modulo N" On | Chegg.com To summarize: solving for x in the congruence ax 1 mod m is equivalent to solving for integers x and y in the equation ax my = 1 (be sure you see why!), and the latter equation can be solved without any guesswork by reversing euclid's algorithm on a and m when (a; m) = 1. Recall: the congruence modulo m on z is an equivalence relation and the equivalence class of z e z, {ує z : y x (mod m)) of z. claim: now one can prove that if tn proof.

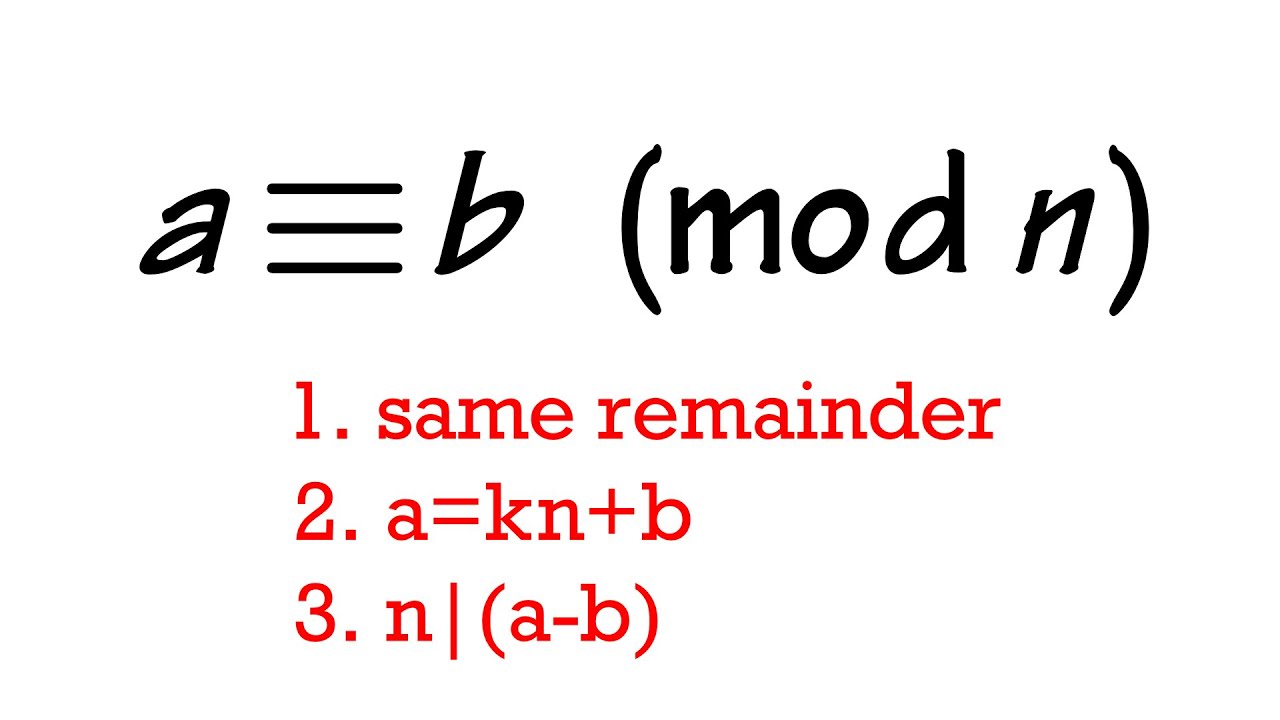
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence